Reflexive space
In functional analysis, a Banach space (or more generally a locally convex topological vector space) is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.
Contents |
Definitions
Normed spaces
Suppose X is a normed vector space over R or C. We denote by X ′ its continuous dual, i.e. the space of all continuous linear maps from X to the base field. As explained in the dual space article, X ′ is a Banach space. We can form the double dual X ′′, the continuous dual of X ′. There is a natural continuous linear transformation
- J : X → X ′′
defined by
- J(x)(φ) = φ(x) for every x in X and φ in X ′.
That is, J maps x to the functional on X ′ given by evaluation at x. As a consequence of the Hahn–Banach theorem, J is norm-preserving (i.e., ||J(x)|| = ||x|| ) and hence injective. The space X is called reflexive if J is bijective. (This implies that a reflexive normed space is a Banach space, since X must be isometric to the complete space X ′′.) The space X is called quasi-reflexive (of order d) if X ′′/J(X) has finite dimension d.
Locally convex spaces
When X is a locally convex topological vector space, the continuous dual X ′ can be equipped with the strong topology β(X ′, X), the topology of uniform convergence on bounded subsets of X. Let 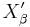 denote this topological vector space, called the strong dual of X. When the canonical embedding J of X into the dual of
denote this topological vector space, called the strong dual of X. When the canonical embedding J of X into the dual of 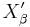 is bijective, then X is said to be semi-reflexive. If, in addition, the topology on X coincides with the strong topology β(X, X ′β), then X is said to be reflexive.
is bijective, then X is said to be semi-reflexive. If, in addition, the topology on X coincides with the strong topology β(X, X ′β), then X is said to be reflexive.
Note When applied to normed spaces, the definitions in this section coincide with the notion of reflexivity for normed spaces. Indeed, the norm topology on the dual X ′ of a Banach space X coincides with the strong topology β(X ′, X), so that, as topological vector space, the normed space X ′ is the strong dual of X. Also, the norm topology on X coincides with β(X, X ′). Therefore, X is reflexive as topological vector space if and only if it is reflexive as normed space, namely, when the injection J is bijective.
Examples
Every finite-dimensional normed space is reflexive, simply because in this case, the space, its dual and bidual all have the same linear dimension, hence the linear injection J from the definition is bijective, by the rank-nullity theorem.
The Banach space c0 of scalar sequences tending to 0 at infinity, equipped with the supremum norm, is not reflexive. It follows from the general properties below that ℓ1 and ℓ∞ are not reflexive, because ℓ1 is isomorphic to the dual of c0, and ℓ∞ is isomorphic to the dual of ℓ1.
All Hilbert spaces are reflexive, as are the Lp spaces for 1 < p < ∞. More generally: all uniformly convex Banach spaces are reflexive according to the Milman–Pettis theorem. The L1(μ) and L∞(μ) spaces are not reflexive (unless they are finite dimensional, which happens for example when μ is a measure on a finite set). Likewise, the Banach space C([0, 1]) of continuous functions on [0, 1] is not reflexive.
The spaces Sp(H) of operators in the Schatten class on a Hilbert space H are uniformly convex, hence reflexive, when 1 < p < ∞. When the dimension of H is infinite, then S1(H) (the trace class) is not reflexive, because it contains a subspace isomorphic to ℓ1, and S∞(H) = L(H) (the bounded operators) is not reflexive, because it contains a subspace isomorphic to ℓ∞ (in both cases, the subspace can be chosen to be the operators diagonal with respect to a given orthonormal basis of H).
Every finite-dimensional Hausdorff topological vector space is reflexive, because J is bijective by linear algebra, and because there is a unique Hausdorff vector space topology on a finite dimensional vector space.
Montel spaces are reflexive locally convex topological vector spaces.
Every semi-reflexive normed space is reflexive.[1] A (somewhat artificial) example of a semi-reflexive space, not reflexive, is obtained as follows: let Y be an infinite dimensional reflexive Banach space, and let X be the topological vector space (Y, σ(Y, Y ′)), that is, the vector space Y equipped with the weak topology. Then the continuous dual of X is the set Y ′ and bounded subsets of X are norm-bounded, hence the Banach space Y ′ is the strong dual of X. Since Y is reflexive, the continuous dual of X ′ = Y ′ is equal to the image J(X) of X under the canonical embedding J, but the topology on X is not the strong topology β(X, X ′), that is equal to the norm topology of Y.
Properties
If a Banach space Y is isomorphic to a reflexive Banach space X, then Y is reflexive.
Every closed subspace of a reflexive space is reflexive. The dual of a reflexive space is reflexive. Every quotient of a reflexive space is reflexive.
The promised geometric property of reflexive Banach spaces is the following: if C is a closed non-empty convex subset of the reflexive space X, then for every x in X there exists a c in C such that ||x − c|| minimizes the distance between x and points of C. (Note that while the minimal distance between x and C is uniquely defined by x, the point c is not. The closest point c is unique when X is uniformly convex.)
Let X be a Banach space. The following are equivalent.
- The space X is reflexive.
- The dual of X is reflexive.
- The closed unit ball of X is compact in the weak topology.(This is known as Kakutani's Theorem.)[2]
- Every bounded sequence in X has a weakly convergent subsequence.[3]
- Every continuous linear functional on X attains its maximum on the closed unit ball in X. (James' theorem)
A reflexive Banach space is separable if and only if its dual is separable. This follows from the fact that for every normed space Y, separability of the dual Y ′ implies separability of Y.
See also
- A generalization which has some of the properties of reflexive spaces and includes many spaces of practical importance is the concept of Grothendieck space.
- Reflexive operator algebra
Notes
- ^ Schaefer 5.6
- ^ Conway, Theorem V.4.2, p.135.
- ^ Since weak compactness and weak sequential compactness coincide by the Eberlein–Šmulian theorem.
References
- J.B. Conway, A Course in Functional Analysis, Springer, 1985.
- Schaefer, Helmuth H. (1966). Topological vector spaces. New York: The MacMillan Company. ISBN 0-387-98726-6.